Find the three missing numbers to unlock the vortex!
28 Jun 2013
27 Jun 2013
The Productivity of Numbers: Upper Secondary Mathematics Competition Question
In the previous question, we looked at the digital addition of natural numbers and introduced the concepts of digital sum, digital root and ‘additude’. In this question, we’re going to look at the multiplicative versions of the same concepts.
Take any natural number and multiply together its digits; this gives us its digital product (dp). Repeat this process until we reach a single-digit number; this is its multiplicative digital root (which is a mouthful, so abbreviated to mdr). The number of iterations needed to reach this mdr, we shall call its ‘productivity’.
For example, let’s take the number 3456, then the dp(3456) = 3x4x5x6 = 360. Then, the dp(360) = 0, giving us the mdr(3456) = 0 and the productivity is equal to 2. As a reminder, the additive digital sums form the sequence (3456, 18, 9) so that the additive digital root is equal to 9 and the additude is 2.
Find all those natural numbers below 1000 that have the multiplicative digital root, the productivity, the additive digital root and the additude, all equal to 2.
26 Jun 2013
Numbers with Additude: Middle Secondary Mathematics Competition Question
Every number has additude! Take a natural number (in base 10) and add together its digits; this gives us its digital sum. Continue this process to obtain a sequence of digital sums that terminates with a single-digit number; this is known as the digital root of the original number (and, of course, the digital root of all the numbers in the sequence). Now, the number of iterations needed to reach the digital root is to be called the additude of the starting number.
For example, starting with the number 5678 we obtain the sequence (5678, 26, 8). So the number 5678 has a digital root of 8 and an additude of 2. The number 8 has a digital root of 8 and an additude of 0.
Find the smallest possible number that has a digital root of 7 and an additude of 3.
For example, starting with the number 5678 we obtain the sequence (5678, 26, 8). So the number 5678 has a digital root of 8 and an additude of 2. The number 8 has a digital root of 8 and an additude of 0.
Find the smallest possible number that has a digital root of 7 and an additude of 3.
Some News: Dynamic Views, Stats and Stumblers
I am in the middle of making a few minor changes to this website, so time for an update and a round-up of the first six months online.
New Dynamic Views
You will notice a new navigation bar in the header. As the site has grown, many questions now lie buried deep within the Archive; and how many people browse the Archive? So the new links are there to group together questions at about the same difficulty level. However, those links also take you to a new way to view Gifted Mathematics!
Google calls these Dynamic Views and you can select your favourite View by using the dropdown menu on the far left. I have chosen to use Snapshots merely because it shows thumbnails of all the relevant images within a post. Flipcard looks cleaner, and Mosaic is fun, but they only pick up the first image as their default thumbnail so an important diagram related to the question is often missing. Another great advantage of Dynamic Views is that it automatically scales to be optimal for most devices.
However, Dynamic Views has some drawbacks, the main one being that many gadgets and apps do not currently function properly. So, for the moment, I am using Dynamic Views as an overlay and the default layout will remain unchanged. If I see that there is a lot of use of this feature I may consider making it the new standard layout. Be aware that in my own testing I have found that the Google+ Comments box is not working within Dynamic Views. I shall look into this more deeply but, for the moment, to see and respond to comments just refresh the page you are on and it will automatically flip back to the standard layout. Any feedback on this would be welcomed.
Talking of Comments...
I think it worth a reminder that the newly integrated G+ Comments system is working well, but the only place you will see all the comments and shares is on the website. For example, when I publish a new question the first place it is posted to is the Mathematics Competition Community on G+. If somebody shares that post to another community, or publicly, then comments on that shared post will not appear in my original G+ post but they will appear on the original question at this website. Think of it as the aggregator of all comments related to that question. Because of the scale of G+ it is not uncommon to find a comment thread that gathers momentum outside of my Community. Also, comments made on the website itself do not appear on G+ unless they are replies to existing comments.
Thank You Stumblers!
I have been using StumbleUpon for many years; admittedly rather on-and-off but it has always been my favourite bookmarking website. So it is no surprise that I am still using it with a Mathematics Competitions List of links to this and other websites related to various maths competitions. You will also often find links to useful websites with apps, scripts and tables of mathematics that are helpful in playing around with some of the questions I set.
Well, my one moan is that StumbleUpon needs to improve a bit on the way they present data to the user. If I go to my homepage, I find that I have only 5 Followers – yes, I know, deeply sad. However, only when I have a look at my Lists page do I discover that the Mathematics Competition List has nearly 600 followers! So, a big “Thank You!” to you Stumblers; and a wee moan at SU for not (yet) showing that data on my profile page.
Number Crunching
After six months online, this Gifted Mathematics website has received over 37,000 pageviews and 1.4k shares on Google+. The G+ profile page has about 2.2k votes and nearly 800 people in its circles. The Mathematics Competitions Community has nearly 700 members and growing. All I need is a few more people to answer the Prize Maths Quiz questions!
Thanks to everyone who has participated, shared, downloaded question papers or just given a thumb up!
Richard
Owner of GiftedMathematics.com
25 Jun 2013
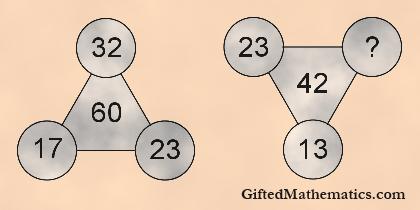
Number Puzzle 11-14: Upper Primary Mathematics Competition Question
This is easier than the number puzzle I posted earlier today - or at least I think so. However, as you can see, they share some genetic material! Have fun!
Find the missing number. There is one solution. If you find different ingenious solutions then feel free to share them below.
Find the missing number. There is one solution. If you find different ingenious solutions then feel free to share them below.
21 Jun 2013
Prize Maths Quiz: Sum of Divisors (PMQ24)
 |
| Omar Khayyam (1048-1131) |
Find all values of n such that S(n) = 120 and prove that there are no others.
-=o0o=-
In most countries, mathematics competitions tend to be multiple-choice answers in the first round, then numerical answers in the follow-up round. But if you make it beyond these rounds, the questions become longer and harder and you will need to show your full solutions.
Finding an answer is sometimes the easiest part; showing that you have found all the answers is often the hardest part. With this in mind, it is worth doing the above question by hand as it will also be the way you can show that you have found all the solutions.
Enjoy!
20 Jun 2013
Sum of Divisors Equation: Upper Secondary Mathematics Competition Question
Let S(n) be the sum of the divisors of the whole number n, including 1 and n itself. Find all the solutions to the equation
S(n) + 2 = S(n+2)
where 0 < n < 100.
S(n) + 2 = S(n+2)
where 0 < n < 100.
19 Jun 2013
Find the Minimal Product xyz: Middle Secondary Mathematics Competition Question
Let x, y and z be positive integers that have a pairwise gcd(m,n)=1. Find all solutions (x, y, z) such that
x + 2y + 3z = 29
and
3x + 2y + z = 35
What is the minimum value of the product xyz?
x + 2y + 3z = 29
and
3x + 2y + z = 35
What is the minimum value of the product xyz?
General Diagonals in Squares: Lower Secondary Mathematics Competition Question
This is the general case of the question posted earlier.
A NxN grid is drawn so that it has N^2 unit squares where N is an even number. A diagonal within a unit square is a straight line with endpoints at opposite corners of the square - one example is drawn below. You are required to draw such diagonals in such a way that none of them have a point in common; that is, two diagonals cannot overlap and they cannot touch at an endpoint.
What is the maximum number of such diagonals of unit squares that can be drawn within a general NxN grid where N is even?
What is the formula if N is an odd number?
A NxN grid is drawn so that it has N^2 unit squares where N is an even number. A diagonal within a unit square is a straight line with endpoints at opposite corners of the square - one example is drawn below. You are required to draw such diagonals in such a way that none of them have a point in common; that is, two diagonals cannot overlap and they cannot touch at an endpoint.
What is the maximum number of such diagonals of unit squares that can be drawn within a general NxN grid where N is even?
What is the formula if N is an odd number?
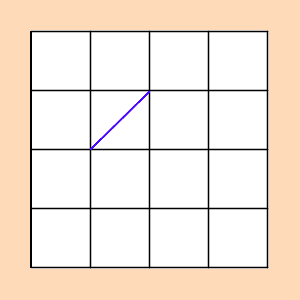
Diagonals in Squares: Upper Primary Mathematics Competition Question
A 4x4 grid is drawn so that it has 16 unit squares. A diagonal within a unit square is a straight line with endpoints at opposite corners of the square - see the image for an example. You are required to draw such diagonals in such a way that none of them have a point in common; that is, two diagonals cannot overlap and they cannot touch at an endpoint.
What is the maximum number of such diagonals of unit squares that can be drawn within this 4x4 grid?
14 Jun 2013
Prize Maths Quiz: A Number Puzzle Within a Code (PMQ23)
Vvw nhrehawa X(p) uadrw wg lpr rwatme sh dgavxkjw qaxguwzf xjol iei tsdigmxsdg cvkaw bb r. Ril iasvvwz jea, wl qf xjs fczfgf gn vrvsymew o, kzmei 1 ≤ o ≤ b, kcpl vvsb glg uul(a,q)=1. Hcj mkeoddm, G(10) = {1, 3, 7, 9} = 4.
Gczucyevs L(30) iah V(43) ofl uipqw nvrf H(55470).
Enjoy!
13 Jun 2013
RSA Public-Key Encryption: Upper Secondary Mathematics
The idea behind every encryption system is to make communication between two parties secure and secret. The systems we have looked at this week involve a method, or algorithm, and a key; sometimes the encryption and decryption keys are the same, sometimes different. The task of anybody trying to intercept the communication is to try to discover both the algorithm and the encryption/decryption keys.
In 1977 a counter-intuitive discovery was published: that it was possible to devise a system where the encryption key was made public with only the decryption key kept private. This became known as RSA Public-Key Encryption and is still in use today.
Rather than thinking about it in terms of keys, imagine we have a lock-and-key system. Zeta receives all her communication via a courier system that places every message inside a box, locks it and then sends it to her. Zeta has created many copies of her private lock and distributes them throughout the world. Anybody who wishes to communicate with her places their message in a courier box, finds one of Zeta’s special locks and then closes the box securely using that lock. Anybody can do this, but only Zeta holds the key that unlocks the box! The encryption locks are public but the decryption key is private.
The mathematics behind this system involves knowledge of prime numbers and modular arithmetic. Let me go through one example, then you can try a similar question.
12 Jun 2013
The Undecipherable Cipher: Middle Secondary Mathematics

The weakness of the substitution ciphers used in the first two questions is that the distribution of letter frequencies remains intact. However, there is a very simple yet powerful method that changes the distribution of letters, thereby making the ciphertext much harder to crack.
The most common letters in the English language form the sequence ETAON RISHD; the most common double letters are TH and HE; and the most common first letter of a word is T. If blank spaces are encoded, then the ”space” becomes the most popular symbol (for example, in Unicode the “space” is encoded as U+2420). All this statistical information is used to crack simple substitution ciphers. However, what would happen if we used a sequence of different substitutions? A 16th century French diplomat, Blaise de Vigenère, perfected just such an encryption method that now bears his name.
Imagine that instead of one alphabet disk we have a sequence of them. Both the plaintext and ciphertext letters are in alphabetical order. Now, imagine picking a keyword, let’s start with something simple such as BYTE. Set the first wheel so that the plaintext letter A is encoded into the letter B; then set the second wheel so that A encodes into Y; then set the third and fourth wheels to T and E. No further wheels are needed in this case. Now, take your plaintext and encode the first letter using the first wheel, encode the second letter using the second wheel, and so on. Once you reach the end of your keyword start from the beginning again; in this way the fifth letter of the plaintext will be encoded using the first wheel again. This very simple method destroys the frequency distribution of the letters in the plaintext.
Without computers, the Vigenère Cipher is extremely difficult to crack. Indeed, if the keyword is very long - say, a whole poem - or at least longer than the actual message, then it is impossible to crack! It became so famous as to be called the Undecipherable Cipher. However, using some brute force computing and a fairly short keyword, some new statistical patterns emerge.
11 Jun 2013
Cracking Codes: Lower Secondary Mathematics
As a student, I first came across it as a teenager attending the Mathematics Masterclasses at the Royal Institution. I later taught a similar course at a Gifted Summer School. Indeed, it makes a great project for gifted maths clubs, summer schools and any other form of extension to the standard curriculum.
The first puzzle was a simple substitution cipher often called the Caesar Shift Cipher or rot-N, where N denotes the number of letters by which the alphabet has been shifted, or rotated when using an alphabet wheel.
The problem with merely shifting the alphabet is that there are very few ways to encode a message; if you get one letter correct, the whole message appears! Assuming a 26-letter alphabet, the simple shift cipher has only 25 settings - the 26th setting is the original plaintext. However, if we substitute the letters randomly, we have 26! possible permutations and that’s over 4x1026 potential ciphertexts – over 40,000,000,000,000,000,000,000,000 in longhand.
This Substitution Cracking Tool from Simon Singh, and its frequency analysis, will help you bring such a large number down to size.
Ciphertext 1
CJZTB OIXTT LJQJKRX XTCHKRX SAKVCABL MJOI LJYTL TUHRK OA OIALT AG R XJCIO RBCKTY OXJRBCKT OITB OIT RXTR AG OIT KRXCTLO SAKVCAB JL TUHRK OA OIT LHQ AG OIT RXTRL AG OIT OMA LQRKKTX ABTL
10 Jun 2013
8 Jun 2013
Winners of PMQ16 and PMQ17
My apologies for being a little lax with these announcements. I'm often waiting for replies and then it slips down the list of things to do. My excuse is that sometimes the questions take a long time to compose! This weekend, I shall be resending emails and hopefully come right up to date.
One thing to remind everyone who has sent in a PMQ answer. You will immediately receive an automated reply; this is done so that you know that your email has been received and not to send another one! Also, when you see this, please add the domain to your white list so that the prize winners announcement doesn't get caught in whatever spam trap you may have.
OK, without any further rambling...
PMQ16 Winners
Jeffrey Bond from the USA
M.K.
These were the only two entries that had at least one of the questions correct. If you wish to try the question, then just go to PMQ16 - but be careful as the answers are in the comments section!
PMQ17 Winners
Chris Breederveld from The Netherlands
Tan Qi Huan from Malaysia
You can try the question at PMQ17. Be careful, the most common mistake in this puzzle was to forget that there is an even prime!
Congratulations to all the winners and thanks to everyone who participated.
If any of the above winners wishes to add a link to their personal page such as G+ or Facebook, then please get in touch or send me a PM within G+. Thanks.
7 Jun 2013
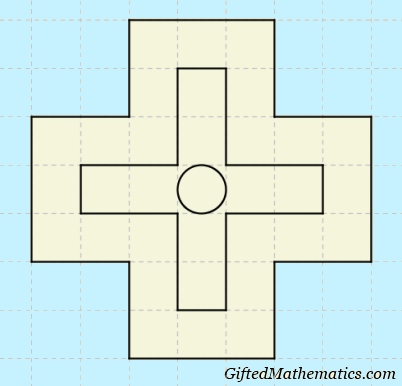
Prize Maths Quiz: A Large Cross of Numbers (PMQ22)
This is an extended version of previous Cross-Number Puzzles published here and here.
This time, the aim is to insert sixteen distinct 3-digit numbers into the grid such that every number is either a perfect square or cube.
Every number must be greater than 99, so there are no leading zeros. Numbers are read either left-to-right or top-to-bottom. The larger outer cross requires twelve numbers and the inner cross has space for four numbers; the circle in the centre will have a digit that is the first digit of two numbers and the last digit of two other numbers.
I have found one solution, but there may be more.
When submitting your answers, just write out a chain of numbers going clockwise round the outer cross, for example, starting at the top, 441 – 125 – 529 – 961 – 361... and so on. Then write the four numbers in the centre cross.
Have fun!
6 Jun 2013
An Average Question: Upper Secondary Mathematics Competition Question
Calculate the average value of the expression
(a - b)2 + (b – c)2 + (c – d)2 + (d – e)2 + (e – f)2
over all possible arrangements of (a, b, c, d, e, f) of the six numbers 2, 3, 5, 12, 15, 16.
On the face of it, this seems like a long hard slog of enumerating 6! = 720 different arrangements of the six numbers. However, there is a shortcut!
This question has been adapted from a UKMT Cayley paper. This means it is aimed at the best lower secondary mathematicians in the UK – only the top 500 are invited to participate – so I think it should be solvable by upper secondary students. I’d rate this at about 10-15 minutes of writing and thinking time.
(a - b)2 + (b – c)2 + (c – d)2 + (d – e)2 + (e – f)2
over all possible arrangements of (a, b, c, d, e, f) of the six numbers 2, 3, 5, 12, 15, 16.
On the face of it, this seems like a long hard slog of enumerating 6! = 720 different arrangements of the six numbers. However, there is a shortcut!
This question has been adapted from a UKMT Cayley paper. This means it is aimed at the best lower secondary mathematicians in the UK – only the top 500 are invited to participate – so I think it should be solvable by upper secondary students. I’d rate this at about 10-15 minutes of writing and thinking time.
5 Jun 2013
Equilateral Triangle in a Square: Middle Secondary Mathematics Competition Question
If the sides of the triangle are each 10 units in length, find the area of the square.
You may leave it as an exact value. As most competitions do not allow calculators, you would have no choice in this. However, in this case, you can obviously calculate the answers and, at the very least, check that the square is actually larger than the triangle.
4 Jun 2013
Cross-Number Puzzle 2: Lower Secondary Mathematics Competition Question
The square grid is the same as in the previous Cross Number puzzle. However, this time the aim is to complete the grid with four distinct 3-digit square numbers.
What is the smallest possible sum of these four numbers?
The numbers are read in the standard way, either left-to-right or top-to-bottom. Each number must be greater than 99, so no leading zeros.
As an extension, how many solutions are there to the general problem of fitting four distinct 3-digit square numbers into the grid?
What is the smallest possible sum of these four numbers?
The numbers are read in the standard way, either left-to-right or top-to-bottom. Each number must be greater than 99, so no leading zeros.
As an extension, how many solutions are there to the general problem of fitting four distinct 3-digit square numbers into the grid?
3 Jun 2013
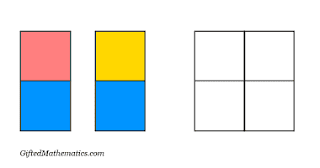
A Square Tile: Upper Primary Mathematics Competition Question
You have two rectangular tiles and wish to place them inside the larger square. One tile is blue and red, the other is blue and yellow.
How many different patterns can you make?
How many unique patterns can you make? In this case, treat all rotational symmetries as one unique pattern; just as you would if it was a real tile that you could rotate in your hand.
Subscribe to:
Posts (Atom)