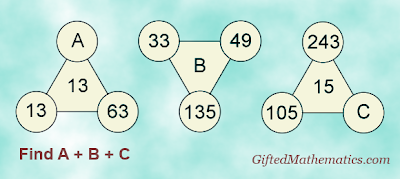
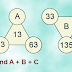
31 Aug 2013
29 Aug 2013
IrMO 1997 P2 Q1: Abundant Numbers: Upper Secondary Mathematics Competition Question
Given a positive integer n, denote by sigma(n) the sum of all positive integers which divide n. [For
example, sigma(3) = 1 + 3 = 4, sigma(6) = 1 + 2 + 3 + 6 = 12, sigma(12) = 1 + 2 + 3 + 4 + 6 + 12 = 28].
We say that n is abundant if sigma(n) > 2n. (So, for example, 12 is abundant).
Let a, b be positive integers and suppose that a is abundant. Prove that ab is abundant.
[IrMO 1997 Paper 2 Question 1]
A Sequence of Prime Factors: Upper Secondary Mathematics Competition Question
Let f(x) be the sum of the prime factors of the positive integer x, including repeated factors. For example, f(20)=f(2x2x5)=2+2+5=9. Note that f(1)=0 and f(p)=p if p is prime.
Let g(x) be the function g(x)=f(ax+b), where a and b are positive integers. If we iterate g we obtain the sequence g0=x, g1=f(ag0+b) and gn=f(agn-1+b). Such sequences always end in a cycle of length L. Some of these sequences terminate at a fixed point P with a cycle length of 0.
For example, if g(x)=f(3x+1) and x=14 we get the sequence {14, 43, 20, 61, 29, 17, 17} which terminates at the fixed point 17.
Let's look specifically at the function g(x)=f(5x+3).
a) Calculate the sequence generated from x=40 and find its value of L.
b) Find the two fixed points of this sequence that are both less than 100.
Note that such sequences have not been exhaustively analysed and there are a number of open questions that I will discuss in another post.
28 Aug 2013
IrMO 1995 P2 Q5: Upper Secondary Mathematics Competition Question
For each integer n such that n = p1p2p3p4, where p1, p2, p3, p4 are distinct primes, let
d1 = 1 < d2 < d3 < ... < d15 < d16 = n
be the sixteen positive integers that divide n.
Prove that if n < 1995, then d9 - d8 ≠ 22.
[IrMO 1995 Paper 2 Question 5]
d1 = 1 < d2 < d3 < ... < d15 < d16 = n
be the sixteen positive integers that divide n.
Prove that if n < 1995, then d9 - d8 ≠ 22.
[IrMO 1995 Paper 2 Question 5]
Terminating Primes: Middle Secondary Mathematics Competition Question
Let s(n) be the sum of the proper factors of a positive integer n; this is the sum of all the factors of n, including 1 but excluding n itself. Let s0=n, s1=s(n), s2=s(s(n)) and so on, thereby creating the sequence {s0, s1, s2, ...}.
If n is a prime number p, then s(p)=1 and s(s(p))=0, thus terminating the sequence. As most such sequences terminate in this way, it is normal to terminate the sequence at the first prime number.
a) Calculate the terminating prime number for the starting value of n=12.
b) Find all possible sequences such that s6=7.
c) Prove that it is not possible for a sequence to terminate with a 5, unless s0=5.
These types of sequences are still being researched and they do not all terminate in the manner described above. Try n=276 and see what happens. Have fun!
27 Aug 2013
Amicable Numbers: Lower Secondary Mathematics Competition Question
The sum of the proper divisors of a positive integer n, spd(n), is the sum of the factors that includes 1 but excludes n itself.
A pair of numbers, m and n, is said to be amicable if spd(n)=m and spd(m)=n. The smallest such pair of numbers is 220 and 284.
Which of the following numbers form another pair of amicable numbers?
1174, 1184, 1210, 2394, 2924.
A pair of numbers, m and n, is said to be amicable if spd(n)=m and spd(m)=n. The smallest such pair of numbers is 220 and 284.
Which of the following numbers form another pair of amicable numbers?
1174, 1184, 1210, 2394, 2924.
An Odd Sequence: Middle Secondary Mathematics Competition Question
A function T(x) is defined as follows, where x is a positive integer:
If x is even, divide x by 2;
If x is odd, calculate the sum of all the factors of x (including 1 and x itself).
Repeat these rules, thereby creating a sequence of numbers. Let S0=x, S1=T(x), S2=T(T(x)) and so on, so that Sn=Tn(x). Also, let m be the first iteration at which Sm=Tm(x)=1. Note that T(1)=1, so we terminate the sequence at the first 1 we encounter.
For example, if x=5, S0=5, S1=6, S2=3, S3=4, S4=2, S5=1. This results in the sequence {5, 6, 3, 4, 2, 1}, so that for x=5, m=5.
a) Find the value of m for x=121.
b) Find the values of x for which m=7.
One open question to ponder is whether such a sequence terminates for every starting value of x.
26 Aug 2013
More Brilliant Numbers: Lower Secondary Mathematics Competition Question
A brilliant number is defined as a whole number that is the product of just two prime factors, both of which have the same number of digits in base 10. For example, 21 (=3x7) and 25 (5x5) are 2-digit brilliant numbers but 77 (=7x11) is not; 143 (=11x13) is a 3-digit brilliant number.
Find the minimal and the maximal 3-digit brilliant numbers.
You may wish to try this question first: calculate the minimal and maximal 2-digit brilliant numbers.
Brilliant Numbers: Upper Primary Mathematics Competition Question
A brilliant number is defined as a whole number that is the product of just two prime factors, not necessarily distinct, both of which have the same number of digits in base 10. For example, 21 (=3x7) is a 2-digit brilliant number but 77 (=7x11) is not.
Find the smallest and the largest 2-digit brilliant numbers.
23 Aug 2013
Prize Maths Quiz: Another Unfair Pizza Puzzle (PMQ33)
After a week of slicing up cakes and pizzas, here’s a PMQ with a similar theme.
Take a circle and randomly draw three distinct diameters, thereby partitioning the circle into six sectors. What is the probability that two of the sectors each has an area that is at least a quarter of the circle?
Just a note, that you may pick any random method, e.g., a random number generator for the angle of a diameter with respect to some zero point. Depending on your chosen method, you may end up with either a discrete or continuous function; it will be interesting to see how their results differ, and I shall accept both versions. You may, of course, come up with an altogether different method!
Have fun!
22 Aug 2013
IrMO 1994 P1 Q2: A Centroid of Centroids: Upper Secondary Mathematics Competition Question
Let A, B, C be three collinear points, with B between A and C. Equilateral triangles ABD, BCE, CAF are constructed with D and E on one side of the line AC and F on the opposite side. Prove that the centroids of the triangles are the vertices of an equilateral triangle. Prove that the centroid of this triangle lies on the line AC.
[IrMO 1994 P1 Q2]
[IrMO 1994 P1 Q2]
Partitioning a Circle: Upper Secondary Mathematics Competition Question
This is the last of this week’s excursions into pizzas and cakes. In essence, these questions have been about the partitioning of two- and three-dimensional figures, so let’s abandon the culinary analogies for this one.
Take a circle and distribute n distinct points around its circumference. Join each point to every other point with a chord. The circle has thus been partitioned into a number of non-overlapping regions. Let R(n) be the maximum number of regions that can be created.
Given that R(n) is a quartic polynomial, or otherwise, find R(n) and hence calculate R(10).
21 Aug 2013
Slicing Jupiter: Middle Secondary Mathematics Competition Question
What is the maximum number of pieces of cake that can be made with 10 planar cuts?
Let’s take a spherical cake, somewhat like the Jupiter layer cake in the image, and each planar knife cut slices the cake into two pieces. We’ve met this problem before, but beyond 4 or 5 slices trying to think geometrically can be a brain ache - unless you are gifted in spatial reasoning! However, the general formula for the maximum number of pieces N(p) after p cuts is just a cubic polynomial. Find this general formula and solve the problem!
[Note that the Jupiter Cake is for real and can be found at Cakecrumbs.]
[Note 2. The slice taken in the diagram, showing the inner layers, is not a planar cut.]
8 Slices of Pizza: Mathematical Puzzle
Half a pizza is never enough – especially if, like Brenda, you actually had less than half. So, Alice and Brenda were back in the kitchen on a mission, opening all the remaining pizza boxes.
“Found one!” beamed Brenda. “This time, let me cut it.” Alice looked sceptical, but thought it was fair enough. Brenda first cuts it in exactly the same way as Alice did, with two perpendicular cuts passing through a point that was not the centre of the circular pizza but lay within it. Before Alice could utter a word, Brenda cut her short, “But now I’m going to make two more cuts.”
Brenda’s two cuts went through the same common point and bisected the right-angles. There were now 8 slices of pizza, as shown in the diagram. “Now, let’s number each slice in sequence from 1 to 8. Would you like the even-numbered slices or the odd-numbered ones?” Alice looked at the pizza and thought... and thought... “It’ll get cold!” said Brenda impatiently. “Cold-er!” was Alice’s laconic reply.
So which slices should Alice take? To make the diagram easier to look at, the even-numbered slices are in red and the odd-numbered slices in white.
Red or White?
Unequal Slices of Pizza: Middle Secondary Mathematics Competition Question
Alice and Brenda stood transfixed as a tower of pizza boxes was delivered and laid out on the kitchen table. The smell of freshly baked dough wafted through the kitchen, enveloping the girls in a kind of spell. “Let me! Let me!” cried Alice, as she opened the first box.
“Hey, Brenda! Look! They forgot to cut this one into slices.” Before Brenda had a chance to register the seriousness of the crime, Alice had found the pizza slicer and was ready to commence surgery. With two clean cuts, Alice divided the pizza into four slices.
“Alice... that’s not really in the centre, is it?!” Brenda was most disappointed with her friend’s eye for geometric precision.
“Mmm... you’re right. Never mind; I’ll take the big slice and the small one. That looks fair!” Alice waltzed off with her plate full of pizza. Brenda stared at her two pieces, certain that she’d been diddled.
Was the division fair? If not, how much more pizza did Alice take?
The diagram shows Alice’s off-centre cuts. The lines AB and CD are perpendicular and cross at point P. Let AP=a, BP=b, CP=c and DP=d, with d > b > a > c. Alice takes the slices BPD and APC while Brenda has the other two. Find an expression for how much extra pizza Alice has compared to Brenda.
20 Aug 2013
Radius and Chords: Middle Secondary Mathematics Competition Question
A circle of radius R has two perpendicular chords intersecting at point P, that lies within the circle.
If AP=4, BP=6 and CP=3, find the length DP and hence the radius R of the circle.
General Pizza Slicing: Middle Secondary Mathematics Competition Question
Find the maximum number of slices of pizza that can be obtained using 20 straight-line cuts?
This is an extension to the earlier Pizza Slices problem. Let’s assume that a pizza is a flat two-dimensional circle. A cut is a straight-line chord that splits the circle into two regions; thereby creating two slices of pizza. We cannot rearrange the slices between each cut.
What is the general formula for the maximum number of pieces of pizza from N straight-line cuts?
[Edited to 20 cuts to match the G+ posts - as there are no answers as yet, I hope this is not a problem.]
19 Aug 2013
Pizza Slices: Upper Primary Mathematics Competition Question
Given a circular pizza, what is the maximum number of pieces that can be made with just 4 cuts?
A cut with a sharp knife is a straight line which, considered on its own, would split the pizza into two pieces. You are also not allowed to rearrange the pizza pieces between cuts.
You may wish to try the problem with 3 cuts first.
And, just a reminder that pizzas are flat! For the 3D version of this problem, look at the Cake Slicing question.
18 Aug 2013
Slicing Cake: Lower Secondary Mathematics Competition Question
Given a circular sponge cake, what is the maximum number of pieces that can be made with just 4 cuts?
A cut with a sharp knife is a flat plane which, considered on its own, would split the cake into two pieces. You are also not allowed to rearrange the cake pieces between cuts.
You may wish to try the problem with 3 cuts first.
16 Aug 2013
Nordic MC 1993 Q1: Upper Secondary Mathematics Competition Question
Let F be an increasing real function defined for all x, 0 ≤ x ≤ 1, satisfying the conditions
(i) F(x/3) = F(x)/2,
(ii) F(1 − x) = 1 − F(x).
Determine F(173/1993) and F(1/13).
[Nordic MC 1993 Q 1][slightly edited]
Prize Maths Quiz: Tablet Access Codes (PMQ32)
Alice has a new tablet computer. At the login screen, rather than having to input a password, there is a grid of nine points. The login access code is created by dragging your finger from one point to the next in a predefined sequence. You may start at any point and drag your finger to any other point that can be reached directly by a straight line (without going through any intermediate points). You may not use the same point twice.
Assuming that Alice’s access code uses just 4 points (and 3 paths), how many such access codes are possible?
One example is given in the diagram. Also, just to clarify, a direct path between two points is one that does not intersect any other points. So, for example, one cannot go directly from the top-left point to the top-right point; in this case one must pass through the middle-top point. You can do it, but it will count as a 3-points and 2-paths route.
Have fun!
14 Aug 2013
Nordic MC 1988 Q2: Upper Secondary Mathematics Competition Question
Let a, b, and c be non-zero real numbers and let a ≥ b ≥ c. Prove the inequality
When does equality hold?
[Nordic MC 1988 Q2]
When does equality hold?
[Nordic MC 1988 Q2]
13 Aug 2013
Nordic MC 1994 Q4: Middle Secondary Mathematics Competition Question
Determine all positive integers n < 200, such that n2 + (n + 1)2 is the square of an integer.
[Nordic Mathematical Contest 1994 Q4]
Reciprocal Powers: Lower Secondary Mathematics Competition Question
What is the value of the median of the following set of numbers?
1, 21/2, 31/3, 41/4, 51/5
You may leave the value as an expression.
1, 21/2, 31/3, 41/4, 51/5
You may leave the value as an expression.
9 Aug 2013
IrMO 1991 P1 Q4: Upper Secondary Mathematics Competition Question
Eight politicians stranded on a desert island on January 1st, 1991, decided to establish a parliament.
They decided on the following rules of attendance:
(a) There should always be at least one person present on each day.
(b) On no two days should the same subset of politicians attend.
(c) The members present on day N should include for each K < N, (K ≥1) at least one member who was present on day K.
For how many days can the parliament sit before one of the rules is broken?
[IrMO 1991 Paper1 Question 4][slightly edited]
Prize Maths Quiz: Blindfolds and Marbles (PMQ31)
Today, Alice is playing games-mistress with her friend Marcus. To win the game, Marcus must pick two marbles of the same colour.
At the start, there are 6 marbles placed inside a small bowl. They are identical to the touch but 3 are blue and 3 yellow. Two empty pouches lie next to the bowl. The player is then blindfolded, the marbles randomised, and he then picks 3 marbles and places them inside one pouch, with the other 3 marbles going into the other pouch. He is then asked to select one pouch and pick just one marble from that pouch and put it inside the other one. At that point, one pouch will have 2 marbles and the other 4 marbles and the blindfolds can be removed. Marcus cannot see inside each pouch but he can feel which one has 2 and which 4 marbles. Lastly, he selects 2 marbles from just one chosen pouch. If the two colours are the same, he wins, if they are different, he loses.
The question is whether it is better to select the pouch with 2 marbles or 4 marbles? Does it make a difference, and if so, what are the relative probabilities to win?
The game is then repeated, with Alice being the player and Marcus the games-master. The whole process described above is merely to ensure that the player is confident that the game is random and not manipulated by a potentially unscrupulous opponent!
There is a follow-up to this but I shall post it separately.
8 Aug 2013
IrMO 1990 P1 Q6: Upper Secondary Mathematics Competition Question
We recently had a question where considering the parity of the numbers (odd and evenness) speeded up our proof. Here is a question that is explicitly about the parity of numbers.
Let n be a natural number, and suppose that the equation
x1x2 + x2x3 + x3x4 + . . . + xn-1xn + xnx1 = 0
has a solution with each of the xi's equal to either +1 or -1. Prove that n is divisible by 4.
[IrMO 1990 Paper 1 Question 6][edited slightly]
Let n be a natural number, and suppose that the equation
x1x2 + x2x3 + x3x4 + . . . + xn-1xn + xnx1 = 0
has a solution with each of the xi's equal to either +1 or -1. Prove that n is divisible by 4.
[IrMO 1990 Paper 1 Question 6][edited slightly]
7 Aug 2013
Irish MO 1988 P1 Q4: Upper Secondary Mathematics Competition Question
A mathematical moron is given the values b, c, A for a triangle ABC and is required to find the value of a. He does this by using the cosine rule
a2 = b2 + c2 - 2bc.cosA
and misapplying the law of logarithms to this to get
log(a2) = log(b2) + log(c2) - log(2bc.cosA).
He proceeds to evaluate the right-hand side correctly, takes the anti-logarithms and gets the correct answer. What can be said about the triangle ABC?
[ Irish MO 1988 Paper 1 Question 4]
The wording is genuine :-)
IrMO 1989 P1 Q4: Upper Secondary Mathematics Competition Question
Note that 122 = 144 ends in two 4's and 382 = 1444 ends in three 4's. Determine the length of the longest string of equal non-zero digits in which the square of an integer can end.
[IrMO 1989 Paper 1 Question 4]
Fibonacci Locker Code: Middle Secondary Mathematics Competition Question
Larry’s locker has a 4-digit security code. To help him remember it, he chose digits from consecutive numbers in the standard Fibonacci sequence (0, 1, 2, 3, 5 and so on). He noticed that two such 4-digit codes were also prime numbers. Larry chose the larger of the two.
What is the 4-digit code to Larry’s locker?
What is the 4-digit code to Larry’s locker?
6 Aug 2013
AA x BB: Middle Secondary Mathematics Competition Question
I assume the question is fairly self-explanatory! The product of two 2-digit numbers AA and BB is equal to the 4-digit number CCDD, where A, B, C and D are distinct numerals between 1 and 9 inclusive.
Pretty simple with an electronic device, but that's not the point - the point is to try it without one! What is a good method that doesn't involve lengthy enumerations of products?
If we lift the restriction that A, B, C and D must be different numbers, are there any more solutions? Zeros are still not allowed, though!
Working Hours: Upper Primary Mathematics Competition Question
Mr Workalot wakes up at 5:45 am. He sets off to work and arrives at (x + 1) am, he then leaves work at (x – 3) pm.
How many hours does Mr Workalot work today?
Money Sharing: Lower Secondary Mathematics Competition Question
Three friends are sitting at a table and wish to play a money-sharing game. Alice gives half her money to Brenda; then Brenda gives half her new total to Carla; and finally, Carla gives half her current total to Alice.
If the three friends each end up with $10, how much money did they each have at the start?
If the three friends each end up with $10, how much money did they each have at the start?
1 Aug 2013
IrMO 1988 P2 Q3: More Bus Stops! : Upper Secondary Mathematics Competition Question
The question I posted for PMQ30 is a simplified version of a real maths competition problem. This is from Paper 2 of the IrMO 1988; such papers have only three questions so are closer to the IMO than Paper 1. Having said that, I think most solvers will need to go through the process of solving PMQ30 to understand how to construct more complicated networks.
The Question
A city has a system of bus routes laid out in such a way that
(a) there are exactly 11 bus stops on each route;
(b) it is possible to travel between any two bus stops without changing routes;
(c) any two distinct bus routes have exactly one bus stop in common.
What is the number of bus routes in the city?
[IrMO 1988 Paper 2 Question 3]
Prize Maths Quiz: A Bus Network Puzzle (PMQ30)
An airport has a system of bus routes to shuttle passengers between terminals. The system is laid out in such a way that:
(a) there are exactly 3 bus stops on each route;
(b) it is possible to travel between any two bus stops without changing routes;
(c) any two distinct bus routes have exactly one bus stop in common.
What is the number of bus routes in the airport?
The diagram shows the fairly trivial case in which each route has just 2 bus stops; in this case, we only need 3 routes to satisfy all the conditions.
Now, there is an extension to this question. In the past, I have occasionally had a choice of two questions for a PMQ. With hindsight, I suspect this has led to some confusion, so I’m posting the extension here.
Extended Domino Triangles: Upper Secondary Mathematics Competition Question
This is an extension to the previous domino triangles problem; I hope Chris Breederveld doesn’t mind me messing with his puzzle!
In this case, take a full set of dominoes but don’t remove the tiles with blanks. The tiles with blanks can still be used to denote a zero. For example, the tile [2/0] can be used as the fraction 0/2 but obviously not as 2/0! This means that the tile [0/0] is the only one that must be removed as it is effectively useless.
Now the question is essentially the same as before. Starting with the tile [6/6] at the top of the triangle, every tile-fraction is the sum of the two tile-fractions below it. How many unique solutions can you find? Treat reflections as one distinct solution.
The diagram below shows the start of one possible solution. Compare this with the diagram in the previous question.
Subscribe to:
Posts (Atom)