The next Prize Maths Quiz (PMQ4) will be posted on Friday 1 February at 20:20 GMT.
The competition will close, as usual, on the Sunday at 23:59 GMT. Please use our official GMT clock on the right-hand column.
See you Friday!
Don’t forget to follow Gifted Mathematics on Google+, Facebook or Twitter. Shorter questions posted on our Google+ Community and Facebook..
You can also subscribe to our Bookmarks on StumbleUpon and Pinterest.
Many resources never make it onto the pages of Gifted Mathematics but
are stored in these bookmarking websites to share with you.
31 Jan 2013
30 Jan 2013
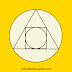
Midweek Maths Puzzle: Heavenly Circles
 | |
| Detail from Medicina Catholica, Robert Fludd (1629-31) |
But enough history, let's look at the picture! Trying to clean up the original I noticed that its negative is far clearer and shows more details, so that's what I've posted. The image shows a large circle at the base, with two medium-sized circles touching each other and the circle beneath them. Finally, the image is crowned by a small circle touching the medium ones.
Prize Maths Quiz: Winners of PMQ2
Again, we had very few entries to our PMQ2 Ice-creams and Cubes competition. However, there were more for PMQ3, so I'm glad to see participation picking up. I will announce the PMQ3 winners once they have replied to my email.
back to PMQ2, I am pleased to announce that our one and only winner is:
Andrew Grounds (USA)
Well done!
PMQ4 will be posted this Friday and I shall announce the exact time during Thursday.
Please make sure you read our full rules on PMQ events and our committment to COPPA guidelines regarding children's online security.
See you Friday!
Don’t forget to follow Gifted Mathematics on Google+, Facebook or Twitter.
You can also subscribe to our Bookmarks on StumbleUpon and Pinterest. Many resources never make it onto the pages of Gifted Mathematics but are stored in these bookmarking websites to share with you.
back to PMQ2, I am pleased to announce that our one and only winner is:
Andrew Grounds (USA)
Well done!
PMQ4 will be posted this Friday and I shall announce the exact time during Thursday.
Please make sure you read our full rules on PMQ events and our committment to COPPA guidelines regarding children's online security.
See you Friday!
Don’t forget to follow Gifted Mathematics on Google+, Facebook or Twitter.
You can also subscribe to our Bookmarks on StumbleUpon and Pinterest. Many resources never make it onto the pages of Gifted Mathematics but are stored in these bookmarking websites to share with you.
28 Jan 2013
Math-e-Monday: Half a Triangle
Most of the questions posted so far have been about numbers, so this week we’re going to concentrate on geometry.
The people who set geometry questions in mathematics competition papers like to mess with your eyes! They are not really optical illusions but, rather like a good magician, you can’t see the whole picture because you’re concentrating only on what you’re being shown. Geometric diagrams do usually show you everything you need but not always everything you know. My advice is to redraw the diagram and fill in everything you know that is related to the question; it could be trigonometry or circle theorems or construction techniques. Then make sure you read the question carefully to check for details that are written down but not illustrated in the given diagram.
Lastly, brush up on some of the more obscure geometric theorems. You can always prove things from first principles, but in a maths test that wastes precious time. It is better to be prepared with a basket full of theorems and then figure out which ones you need.
This is not a PMQ so feel free to discuss this puzzle in the comments section below.
And don’t forget to follow Gifted Mathematics on Google+, Facebook or Twitter.
You can also subscribe to our Bookmarks on StumbleUpon and Pinterest. Many resources never make it onto the pages of Gifted Mathematics but are stored in these bookmarking websites to share with you.
The people who set geometry questions in mathematics competition papers like to mess with your eyes! They are not really optical illusions but, rather like a good magician, you can’t see the whole picture because you’re concentrating only on what you’re being shown. Geometric diagrams do usually show you everything you need but not always everything you know. My advice is to redraw the diagram and fill in everything you know that is related to the question; it could be trigonometry or circle theorems or construction techniques. Then make sure you read the question carefully to check for details that are written down but not illustrated in the given diagram.
Lastly, brush up on some of the more obscure geometric theorems. You can always prove things from first principles, but in a maths test that wastes precious time. It is better to be prepared with a basket full of theorems and then figure out which ones you need.
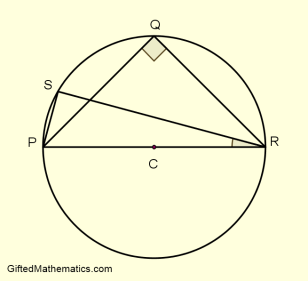
The Question
The diagram above shows a circle centre C (not drawn to scale). The line CQ is perpendicular to the diameter PR. The triangle PQR has double the area of triangle PSR. Find the angle PRS.
This is not a PMQ so feel free to discuss this puzzle in the comments section below.
And don’t forget to follow Gifted Mathematics on Google+, Facebook or Twitter.
You can also subscribe to our Bookmarks on StumbleUpon and Pinterest. Many resources never make it onto the pages of Gifted Mathematics but are stored in these bookmarking websites to share with you.
25 Jan 2013
Prize Maths Quiz: Tinkering With Triangles (PMQ3)
Alice was sitting on the floor toying with her number cards. She was using them to make pretty shapes and then see if she could make number patterns with the shapes.
Her attention was suddenly distracted by a clatter behind her. “What are you doing?” Bill looked like he was in the middle of destroying her torch; though more likely nearer the end.
“Sorry, I was just taking it apart to see how it works.”
“Huh?! There are no moving parts in a torch. Is that your big discovery?”
“Ah, but there is... there's the switch!”
Her attention was suddenly distracted by a clatter behind her. “What are you doing?” Bill looked like he was in the middle of destroying her torch; though more likely nearer the end.
“Sorry, I was just taking it apart to see how it works.”
“Huh?! There are no moving parts in a torch. Is that your big discovery?”
“Ah, but there is... there's the switch!”
24 Jan 2013
Prize Maths Quiz (PMQ3) Announcement for Friday 25 January
The next Gifted Mathematics Prize Maths Quiz shall be PMQ3 and will be posted on Friday 25 January 2013 at 07:03 GMT. The competition will close, as always at 23:59 GMT on the Sunday.
Please use our offical GMT clock in the right-hand column.
Please also read the rules, which have been recently updated and clarified, on our PMQ Prize page.
See You Then!
And don’t forget to follow Gifted Mathematics on Google+, Facebook or Twitter.
You can also subscribe to our Bookmarks on StumbleUpon and Pinterest. Many resources never make it onto the pages of Gifted Mathematics but are stored in these bookmarking websites to share with you.
Please use our offical GMT clock in the right-hand column.
Please also read the rules, which have been recently updated and clarified, on our PMQ Prize page.
See You Then!
And don’t forget to follow Gifted Mathematics on Google+, Facebook or Twitter.
You can also subscribe to our Bookmarks on StumbleUpon and Pinterest. Many resources never make it onto the pages of Gifted Mathematics but are stored in these bookmarking websites to share with you.
23 Jan 2013
Midweek Maths Puzzle: Crossing the Bridge
There are some mathematical questions where the first thing to do is to follow the rules and just ‘play the game’. After a bit of practice you start to figure out the patterns behind the rules. Then you can set about finding a solution.
This is a very old puzzle (old puzzles are old because they remain new, otherwise they’d just be forgotten puzzles) given a fresh lease of life with some computer animation. The rules are simple enough; to get all the people across the bridge in the minimum time. The full rules are on the Crossing the Bridge page.
This is a very old puzzle (old puzzles are old because they remain new, otherwise they’d just be forgotten puzzles) given a fresh lease of life with some computer animation. The rules are simple enough; to get all the people across the bridge in the minimum time. The full rules are on the Crossing the Bridge page.
21 Jan 2013
Math-e-Monday: Prime Combination Lock
Derek has just bought himself a smart new padlock with a combination lock. It is one of those with a 3-digit code that you enter by turning each of the 3 wheels. Derek is playing with it, trying to think of a really clever number that he wouldn’t forget.
He notices that the code was set to 200 and decides to play a game. He picks the middle and right wheels; clicking one of them up a number and the other down a number he gets 291. He continues this until he gets back to 200. Then he tries the same thing with the middle and left wheels, and finally with the left and right wheels.
Derek smiles to himself
a) Write down the prime numbers that Derek finds using his method.
Derek then wants to find out if he can make every possible 3-digit number. He still starts at 200, turns one wheel up and one wheel down, then writes his new number down. But in his next step he can choose any pair of wheels he wishes, not just the two he started with. At each step he writes down his number so as to keep track.
He notices that the code was set to 200 and decides to play a game. He picks the middle and right wheels; clicking one of them up a number and the other down a number he gets 291. He continues this until he gets back to 200. Then he tries the same thing with the middle and left wheels, and finally with the left and right wheels.
Derek smiles to himself
a) Write down the prime numbers that Derek finds using his method.
Derek then wants to find out if he can make every possible 3-digit number. He still starts at 200, turns one wheel up and one wheel down, then writes his new number down. But in his next step he can choose any pair of wheels he wishes, not just the two he started with. At each step he writes down his number so as to keep track.
19 Jan 2013
Prize Maths Quiz: PMQ1 Winners
 |
| PMQ = Perplexing Mathematical Quandary |
All the entries submitted had question (c) wrong, apart from one! There is therefore just one winner of our first Prize Maths Quiz.
Christopher Irwin (USA)
Congratulations!
Your Gifted Mathematics e-Voucher is on its way to you.
Best of luck to everyone for our Prize Maths Quiz PMQ2.
18 Jan 2013
Prize Maths Quiz: Ice-creams and Cubes (PMQ2)
 |
| "Hey, Brenda, finish that PMQ later. Come and look at this!" |
"What's wrong Brenda? Why are you crying?"
"Look!" Brenda pointed to her little money box. "Empty! All the money I made today has gone! I don't know what happened, I couldn't just have lost it. My whole day wasted, and can't even buy some new books!"
Alice quickly added up the few coins left in Brenda's money box. She had already counted hers to the nearest penny. Being a bit of a maths whizz, Alice did a quick calculation and said to herself, "Mmm... that's bizarre, my money is exactly the cube of yours; in pennies, of course."
17 Jan 2013
Solutions and Extensions: The Game of 24 (PMQ1)
Guided Solution to PMQ1
This is the kind of mathematical puzzle that I really like. It is very simple to state, the number of variables is very small and yet it can be excruciating to solve! Remind yourself of the question by opening the Game of 24 PMQ1 in a new tab.
The first two are, obviously, very simple.
a) (7+5)x(6-4) = 12x2 = 24
b) 5x5-(5/5) = 25-1 = 24
If you have different solutions, that's fine, so long as they really come to 24.
c) Now we come to the question that caused most headaches. Rather than just giving a solution - that's what textbooks usually do - I think it important to go through the key steps. That "Aha!" moment is important, and learning how to break out of certain mental restrictions is also a vital part of solving problems, be they maths puzzles or real-life problems. So let me go through how I found the solution.
This is the kind of mathematical puzzle that I really like. It is very simple to state, the number of variables is very small and yet it can be excruciating to solve! Remind yourself of the question by opening the Game of 24 PMQ1 in a new tab.
The first two are, obviously, very simple.
a) (7+5)x(6-4) = 12x2 = 24
b) 5x5-(5/5) = 25-1 = 24
If you have different solutions, that's fine, so long as they really come to 24.
c) Now we come to the question that caused most headaches. Rather than just giving a solution - that's what textbooks usually do - I think it important to go through the key steps. That "Aha!" moment is important, and learning how to break out of certain mental restrictions is also a vital part of solving problems, be they maths puzzles or real-life problems. So let me go through how I found the solution.
Prize Maths Quiz (PMQ) Announcement for Friday 18 January
This week's Prize Maths Quiz (PMQ) will be posted on Friday 18 January at 09:15 GMT.
Solutions will be accepted by email until 23:59 GMT Sunday. Please use the clock on the right-hand column to check the official competition time.
From the experience of the first competition PMQ1, I am slightly changing the rules. Adults and older students can now participate and submit solutions. However, the prizes remain the same: some free places in our Gifted Mathematics Online Classroom for students aged 16 and under. The winners shall be contacted by email and given the prizes as e-vouchers. If they are not young enough themselves to take advantage of our tutorial system, they can give the e-voucher to their child or favourite student. Full details will be given at the foot of the PMQ question on Friday.
Once we receive back the e-voucher, we shall send out a form to be filled in by either a parent or teacher, depending on how the student received the prize, in compliance with COPPA regulations on children's anonymity online. Once we receive the completed form we shall send back an access code to the teaching environment which is run on Edmodo. Once a student has created an account, parents can also create their linked account so that they can supervise and follow the progress of their child. All these systems are in effect to protect children from disclosing personal information. All we at Gifted Mathematics need for the whole process to work is one adult contact email address.
Please also note that all emails received as entries to these Prize Maths Quizzes are deleted once the specific competition email is deactivated and no email addresses are kept. If you wish to receive email updates from us then please sign up using the form on the right. Part of COPPA regulations is that we delete all email addresses as we do not know whether they are from children or adults. We are happy to comply with this in the interest of promoting a safe learning environment.
See you on Friday!
Solutions will be accepted by email until 23:59 GMT Sunday. Please use the clock on the right-hand column to check the official competition time.
From the experience of the first competition PMQ1, I am slightly changing the rules. Adults and older students can now participate and submit solutions. However, the prizes remain the same: some free places in our Gifted Mathematics Online Classroom for students aged 16 and under. The winners shall be contacted by email and given the prizes as e-vouchers. If they are not young enough themselves to take advantage of our tutorial system, they can give the e-voucher to their child or favourite student. Full details will be given at the foot of the PMQ question on Friday.
Once we receive back the e-voucher, we shall send out a form to be filled in by either a parent or teacher, depending on how the student received the prize, in compliance with COPPA regulations on children's anonymity online. Once we receive the completed form we shall send back an access code to the teaching environment which is run on Edmodo. Once a student has created an account, parents can also create their linked account so that they can supervise and follow the progress of their child. All these systems are in effect to protect children from disclosing personal information. All we at Gifted Mathematics need for the whole process to work is one adult contact email address.
Please also note that all emails received as entries to these Prize Maths Quizzes are deleted once the specific competition email is deactivated and no email addresses are kept. If you wish to receive email updates from us then please sign up using the form on the right. Part of COPPA regulations is that we delete all email addresses as we do not know whether they are from children or adults. We are happy to comply with this in the interest of promoting a safe learning environment.
See you on Friday!
16 Jan 2013
MidWeek Maths Puzzle: A Problem With 12 Pins
Alice was helping her Granny Florence make a new dress. Well, Alice was not exactly helping, more like getting in the way.
"Look what I made, Granny!" Alice beamed with pride. "It's a cross made from your pins."
"Very nice, dear, but please don't drop them on the floor as I need them to pin this dress."
"It has an area of 5... erm... pin units made from 12 pins."
"And don't stab yourself either!" Alice did not like being interrupted so carried on as if nothing had been said.
"And if I move these two pins I can make an area of 6 units squared.... and 7... and 8... and..."
"Yes, darling, I know you're very clever. Can you make an area of just 4 units?"
"Look what I made, Granny!" Alice beamed with pride. "It's a cross made from your pins."
"Very nice, dear, but please don't drop them on the floor as I need them to pin this dress."
"It has an area of 5... erm... pin units made from 12 pins."
"And don't stab yourself either!" Alice did not like being interrupted so carried on as if nothing had been said.
"And if I move these two pins I can make an area of 6 units squared.... and 7... and 8... and..."
"Yes, darling, I know you're very clever. Can you make an area of just 4 units?"
14 Jan 2013
Math-e-Monday: Entangled Triplet
It's Monday. It's been a hectic weekend and our Math-e-Monday questions will be on the lighter side of the spectrum. Here's one you can almost do in your head.
If A x B = 5, B x C = 90 and C x A = 2, given that A, B and C are all positive,
find the value of A + B + C
Do try this yourself before checking the answer.
If you're doing this to help with a maths competition, I'd rate this as Lower Secondary standard; and don't even think about reaching for the calculator app!
If A x B = 5, B x C = 90 and C x A = 2, given that A, B and C are all positive,
find the value of A + B + C
Do try this yourself before checking the answer.
If you're doing this to help with a maths competition, I'd rate this as Lower Secondary standard; and don't even think about reaching for the calculator app!
13 Jan 2013
Only Three Dice
They unpacked the game. It was, indeed, a rather simple game; roll the four dice and use any of the four arithmetical operations (and brackets if needed) to make the highest possible number between 1 and 100. The higher the number the more prize money you win and you place your counter on that number so nobody can use it again. But as the game progresses it starts to get harder as many of the top numbers are covered with tokens.
"Oh no!!" shrieked Alice. "I can't find all four dice! I can only find three." Bill thought something really dramatic had just happened, like a spider crawling out of the box. "Maybe we could play something else." he said, trying to put his positive voice to good use. But Alice didn't even reply; she was too busy taking all the games out of her games box to look for the missing die. After a good 10 minutes of rummaging, she admitted defeat.
"Let's play with three dice!!" Alice exclaimed. "Can we still make all 100 numbers, though?" asked Bill. "Probably not," Alice said thoughtfully, "But let's find out!" Bill was just not going to get out of playing Number Quest
The Question
What are the two smallest numbers that cannot be made with just three 6-sided dice using just arithmetic operations?
Also, what are the two largest numbers that cannot be made?
This is not a Prize question, so feel free to comment.
Good Luck!
Maths Questions posted on Mondays, Wednesdays and Saturdays.
Prize Maths Questions (PMQs) posted on Fridays.
>
>
Don't peek at the answers!
>
>
>
>
If you're feeling tired, defocus your eyes on this stereoscopic photograph.
From Wikimedia [public domain]
>
>
Don't miss out on the next Prize Maths Quiz: follow us on Twitter.
11 Jan 2013
Prize Maths Question: The Game of 24 (PMQ1)
![Adrien-Marie Legendre, died 180 years ago 10th January 1833 [Many thanks to http://www-history.mcs.st-and.ac.uk] Adrien-Marie Legendre, died 180 years ago 10th January 1833](http://3.bp.blogspot.com/-4fqUIqoWgfs/UO6kJ-Rw8xI/AAAAAAAAAUM/car71P69mmw/s320/Legendre.jpg) |
| "Every Friday, I get that PMQ feeling." Legendre |
Today she wrote on the board:
Sum to 24
a) 4 5 6 7
b) 5 5 5 5
c) 3 3 8 8
The students had played this game many times before so had no need for the rules. For those of you who haven't, the rules are very simple.
Using all the four single-digit numbers, in any order, make a total of 24 using only the four arithmetical operations and brackets if you need them. No other symbols or numbers are allowed.
It usually takes less than 5 minutes for some of the bright sparks to do all three sums, but on this particular day Miss Abel could see many of her students frowning. "Why was it taking them so long?" she thought.
Finally, Alice put her hand up. "Miss, I can get 25 but not 24. It's impossible!" A murmur of agreement rippled through the class.
Miss Abel was certain she hadn't set anything that hard. She took a quick look at her notes, then looked at the board, then back at her notes, and... she'd written one of the numbers wrongly! She quickly tried to do the sum in her head and, just like Alice, could easily get 25 but not 24. The 5-minute puzzle had turned into a 15-minute challenge.
"I'm surprised nobody has managed to do all of them, so I will leave this with you as a homework puzzle. Right, today's lesson is about..."
Can you do better than Miss Abel and her class? Find all three sums to 24.
The Question
Solve the above problems (a), (b) and (c).
You must include your answer to all three problems in acceptable algebraic format, for example, (3+5)*6/2.
You must submit your answer to the email address below.
Eligibility to Enter
This Prize Maths Question can be entered by students in Primary, Lower Secondary or Upper Secondary school. Basically, anybody 16 years or under can participate. However, if you are under 13 years old and win a prize, we shall require parental approval to join our Online Classroom. Please note that the aim of this website is to help school students master the topics found in school mathematics competitions and challenges. Everyone is welcome to use our free online activities but the Online Classrooms are only for genuine students of school age and not for older students or adults interested in maths games and puzzles. You can go to our Mathematics Competitions Community and participate there.
The Prize
This week's prize is a free place in our Online Classroom for 2 months.
This prize will be awarded to the first correct entry submitted plus four more lucky winners will be selected at random from all other entries. The selection shall be random but weighted towards the quickest replies. This PMQ will close after 24 hours. As this is the first PMQ, it may remain open beyond 24 hours until there are enough winning entries.
Submissions will only be accepted by an email sent to [Competition closed. Email address removed. Feel free to discuss this in the comments below.] DO NOT submit it in the Disqus comments box below. You may discuss the question on Disqus but it will not count as a competition entry. All attempts to send multiple answers or any other form of cheating will result in all such answers being deleted and no prizes being awarded to any such participants, including the original. If you want to guarantee that your email has been sent then just CC it to yourself and check that you have received a copy back. The timestamp on the emails will determine the winners. The above email will be disabled once this PMQ competition has been completed.
Winners will first be notified by email. Once all winners have shown they are genuine students, they shall be announced on this website.
Good Luck!
And once you've submitted your entry, tell your friends about this PMQ!
9 Jan 2013
Fibonacci 2013: Guided Solution
This is the solution to the Fibonacci 2013 problem I posted a few days ago. If you haven't had a go yet, then please try it for yourself first before reading any further!
The reason I call these Guided Solutions is that you will see below both the solution as one would write it down and also some 'thinking boxes' which explain the thought processes that should be going through one's mind. I also include some background information in case you haven't come across such problems before.
So, let's get on with it!
The reason I call these Guided Solutions is that you will see below both the solution as one would write it down and also some 'thinking boxes' which explain the thought processes that should be going through one's mind. I also include some background information in case you haven't come across such problems before.
So, let's get on with it!
Another Fibonacci 2013 Puzzle
 | |
| A Fibonacci Spiral |
The Question
In a Fibonacci sequence of integers, the 2015th term is the same as the 2012th term.
What is the value of the 2013th term?
>
>
>
>
Don't sneak at the answers posted below!
Is there enough information to solve the problem?
>
>
>
>
Any questions, just ask.
>
>
8 Jan 2013
What is GiftedMathematics.com Really About?
In my years of teaching both mathematics and physics, it has become apparent that standards have been slipping for a long time. This is not just a question of dumbing down, but also one of creeping disinterest and boredom. The real tragedy is that it is now affecting both students and teachers. [1]
The one saving grace that I see in the educational landscape is the increase in extra-curricular activities. Looking specifically at mathematics, the Olympiads have set a gold standard for decades. Moreover, the competitions that discover new Olympiad mathematicians are actually open to every student and, I believe, every student benefits from these challenges.
The kind of mathematics that is needed to be successful in these competitions is often very different to what is taught in the standard school curriculum. Mathematics teachers would love to be able to teach this kind of mathematical thinking, but usually lack the time because of the overbearing task of completing that year's syllabus in preparation for official testing.
GiftedMathematics.com is here to fill that gap; to retrain students into the art of mathematical thinking and bring back the joy of solving puzzles that at first glance seem impossible.
GiftedMathematics.com is also here to build up resources for teachers so that they have ready-made lessons and questions and can deliver extra-curricular lessons to students who wish to participate in their national mathematics competition.
The really big idea is that learning to think mathematically is both interesting and rewarding. In some schools, such training is limited to those children considered gifted in mathematics. It is good that such support exists, but in my experience this kind of problem-solving ability is of great benefit to many other students.
When I ran after-school maths clubs, I used to leave the door open to any student; some would realise it was not for them but many would stay and their confidence would light up as they enjoyed playing around with this new kind of maths. Astonishingly, some did better in the 'harder' mathematics competition than in their school exam. How is that possible?
The brain is the nexus of our thinking and our emotions. People often consider these as two different modes of being, but recent research has shown that they are intimately linked; that 'Aha!' feeling is both a moment of intellectual clarity and a small burst of positive emotions. Success is a buzz; a brain buzz!
Every new piece of knowledge understood, every new technique mastered and every problem solved, all are rewarded with these little bursts of neural joy. The path a student takes is guided by these emotional lights. The task of GiftedMathematics.com and all the mathematics competitions throughout the world is to foster that buzz of knowing how to find the unknown.
What do you think?
=====
[1]. I must add a postscript here, that my criticisms of the education system are largely based on my experience in the UK, although I read of the same problems in the USA. I currently live in South East Asia and most students have the same negative reactions to the official syllabus. There are a few bright lights such as Singapore and Hong Kong but, being essentially city-states, they are acutely aware of the importance of their intellectual capital. I find Singapore interesting in that it is based on the UK system but has not gone down the route of dumbing down. If you think all this talk of dumbing down is fabricated, the Cambridge exam board have just recently introduced an award above A-level, know as Pre-U. The mathematics Pre-U syllabus is identical to what I studied at school over 30 years ago, with all the interesting bits put back in; someone, somewhere had to stop the erosion of standards.
The one saving grace that I see in the educational landscape is the increase in extra-curricular activities. Looking specifically at mathematics, the Olympiads have set a gold standard for decades. Moreover, the competitions that discover new Olympiad mathematicians are actually open to every student and, I believe, every student benefits from these challenges.
The kind of mathematics that is needed to be successful in these competitions is often very different to what is taught in the standard school curriculum. Mathematics teachers would love to be able to teach this kind of mathematical thinking, but usually lack the time because of the overbearing task of completing that year's syllabus in preparation for official testing.
GiftedMathematics.com is here to fill that gap; to retrain students into the art of mathematical thinking and bring back the joy of solving puzzles that at first glance seem impossible.
GiftedMathematics.com is also here to build up resources for teachers so that they have ready-made lessons and questions and can deliver extra-curricular lessons to students who wish to participate in their national mathematics competition.
The really big idea is that learning to think mathematically is both interesting and rewarding. In some schools, such training is limited to those children considered gifted in mathematics. It is good that such support exists, but in my experience this kind of problem-solving ability is of great benefit to many other students.
When I ran after-school maths clubs, I used to leave the door open to any student; some would realise it was not for them but many would stay and their confidence would light up as they enjoyed playing around with this new kind of maths. Astonishingly, some did better in the 'harder' mathematics competition than in their school exam. How is that possible?
The brain is the nexus of our thinking and our emotions. People often consider these as two different modes of being, but recent research has shown that they are intimately linked; that 'Aha!' feeling is both a moment of intellectual clarity and a small burst of positive emotions. Success is a buzz; a brain buzz!
Every new piece of knowledge understood, every new technique mastered and every problem solved, all are rewarded with these little bursts of neural joy. The path a student takes is guided by these emotional lights. The task of GiftedMathematics.com and all the mathematics competitions throughout the world is to foster that buzz of knowing how to find the unknown.
What do you think?
=====
[1]. I must add a postscript here, that my criticisms of the education system are largely based on my experience in the UK, although I read of the same problems in the USA. I currently live in South East Asia and most students have the same negative reactions to the official syllabus. There are a few bright lights such as Singapore and Hong Kong but, being essentially city-states, they are acutely aware of the importance of their intellectual capital. I find Singapore interesting in that it is based on the UK system but has not gone down the route of dumbing down. If you think all this talk of dumbing down is fabricated, the Cambridge exam board have just recently introduced an award above A-level, know as Pre-U. The mathematics Pre-U syllabus is identical to what I studied at school over 30 years ago, with all the interesting bits put back in; someone, somewhere had to stop the erosion of standards.
7 Jan 2013
The First Friday Prize Maths Question Announcement
Although just a few days old, I'm kicking off the new year with our first Prize Maths Question (or PMQ). Every week a PMQ will be posted on Friday. Please read the general details on our PMQ page.
To make it fair to everyone in the world, the competition question will be posted at a different time every week. To make it even fairer, (and less annoying not having to come to check all the time) I shall announce the exact time a day or two before.
So here it is... a little early as it's the first time:
This week's GiftedMathematics.com Prize Maths Question will be posted on Friday 11 January at 08:42 GMT.
See you then!
Oh, and not forgetting, general mathematics questions will be posted on Mondays and Wednesday. Tutorial materials will be published as and when they are ready.
To make it fair to everyone in the world, the competition question will be posted at a different time every week. To make it even fairer, (and less annoying not having to come to check all the time) I shall announce the exact time a day or two before.
So here it is... a little early as it's the first time:
This week's GiftedMathematics.com Prize Maths Question will be posted on Friday 11 January at 08:42 GMT.
See you then!
Oh, and not forgetting, general mathematics questions will be posted on Mondays and Wednesday. Tutorial materials will be published as and when they are ready.
5 Jan 2013
Fibonacci 2013
Let's start the new year with some mathematical puzzles with a 2013 theme.
In a Fibonacci sequence each term is equal to the sum of the previous two terms. Obviously, the first two terms have to be chosen, or given, and they define the evolution of the sequence.
The Question
The 7th term of a Fibonacci sequence is 2013. What is the smallest possible integer value of the 3rd term? The first two terms are both positive integers.
>
>
>
>> Try the question before looking at the guided solution.
>
>
>
>
Forgot to mention, I would like to see a method to go with your solution!
>
>
>
>
Guided solution can be found here.
In a Fibonacci sequence each term is equal to the sum of the previous two terms. Obviously, the first two terms have to be chosen, or given, and they define the evolution of the sequence.
The Question
The 7th term of a Fibonacci sequence is 2013. What is the smallest possible integer value of the 3rd term? The first two terms are both positive integers.
>
>
>
>> Try the question before looking at the guided solution.
>
>
>
>
Forgot to mention, I would like to see a method to go with your solution!
>
>
>
>
Guided solution can be found here.
Subscribe to:
Posts (Atom)