Alice was playing around with a peg-board and a jar of elastic bands. She was trying to think up a devilish problem to give Brenda when she finally turned up. Alice had made a real tangled mess and was annoyed with herself for then having to take all the rubber bands off... and then one peg snapped off! She stared at the board, as if willing the peg to jump right back into its rightful place; but it didn't, of course.
However, this now meant that Alice could play with a smaller board. She laid out a perimeter so that she was left with a board of 6 by 6 pins (as shown in the diagram). She had thought of how many elastic bands she'd need if she joined together every pair of pins that were a whole number distance apart, but that had ended up badly. So then she had another idea: join together every pair of pins that are a prime number distance apart. That sounded better! Assuming, of course, that the distance between adjacent pins was a unit length.
So, how many elastic bands will Alice need this time? Do you think she'll have enough of them?!
21 Nov 2013
MEMO 2012 Q2: Upper Secondary Mathematics Competition Question
Let N be a positive integer. A set S is a subset of {1, 2, ..., N} and is called 'allowed' if it does not contain three distinct elements a, b, c such that a divides b and b divides c.
Determine the largest possible number of elements in an allowed set S.
[MEMO 2012 Problem I-2]
[MEMO = Middle European Mathematical Olympiad]
Determine the largest possible number of elements in an allowed set S.
[MEMO 2012 Problem I-2]
[MEMO = Middle European Mathematical Olympiad]
19 Nov 2013
Yin Yang Areas: Lower Secondary Mathematics Competition Question
The diagram is constructed using one circle of radius 4 units, plus pairs of semicircles of radii 1, 2 and 3 units.
Find the ratio of the red : yellow : green : blue areas.
Find the ratio of the red : yellow : green : blue areas.
15 Nov 2013
Integral Network: Professor Pailyn's Mathematical Quest PMQ45
“That was a bit complicated!” Exclaimed Alice, “But what about my original problem? Can we do that now?”
“I think it’s time to recharge those brain cells... with some tea and fruit cake.” Professor Pailyn walked straight past Alice, carrying the tea-tray into the garden.
Alice enjoyed elevenses; it was almost better than breakfast. Alice had never had a proper stroll around the Professor’s garden. As she walked through it with her eyes, she noticed some peculiar structures: a cube within a cube standing on one corner, and what appeared to be a leafy halo suspended in mid-air betwixt two egg-shapes. She wanted to go and find the hidden wires but was too busy eating cake.
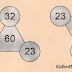
“So... let’s have a little think about your problem. You have four points on a plane, all connected to each other by straight lines. No three points lie on the same straight line so that we have six distinct line segments. You want all six lines to be different whole numbers. Is that right?”
“I think it’s time to recharge those brain cells... with some tea and fruit cake.” Professor Pailyn walked straight past Alice, carrying the tea-tray into the garden.
Alice enjoyed elevenses; it was almost better than breakfast. Alice had never had a proper stroll around the Professor’s garden. As she walked through it with her eyes, she noticed some peculiar structures: a cube within a cube standing on one corner, and what appeared to be a leafy halo suspended in mid-air betwixt two egg-shapes. She wanted to go and find the hidden wires but was too busy eating cake.
“So... let’s have a little think about your problem. You have four points on a plane, all connected to each other by straight lines. No three points lie on the same straight line so that we have six distinct line segments. You want all six lines to be different whole numbers. Is that right?”
14 Nov 2013
Sliced Parallelogram: OEMO 2003 Advanced Q4: Upper Secondary Mathematics Competition Question
In a parallelogram ABCD, let E be the midpoint of the side AB and F the midpoint of BC. Let P be the intersection point of the lines EC and F D.
Show that the segments AP, BP, CP and DP divide the parallelogram into four triangles with areas in 1 : 2 : 3 : 4 ratio.
[OEMO 2003 Federal Advanced Q4]
Show that the segments AP, BP, CP and DP divide the parallelogram into four triangles with areas in 1 : 2 : 3 : 4 ratio.
[OEMO 2003 Federal Advanced Q4]
13 Nov 2013
Sets of Divisors: Middle Secondary Mathematics Competition Question
Let T(n) be the number of divisors of a whole number n that are less than or equal to the square-root of n. For example, T(40) = 4.
Find the smallest number m greater than 2013 where T(m) = 5.
Find the smallest number m greater than 2013 where T(m) = 5.
OEMO 2013 Advanced Q2: Upper Secondary Mathematics Competition Question
12 Nov 2013
Percentage Problem: Upper Primary Mathematics Competition Question
Jamie and Kenny receive the same amount of pocket-money this week. Kenny lends Jamie 10% of his pocket-money. How much more money does Jamie now have compared to Kenny in percentage terms?
Ordered Fractions: Lower Secondary Mathematics Competition Question
9 Nov 2013
Houses in a Row: Professor Pailyn's Mathematics Quest PMQ44
“Look, I’ve invented a problem that I can’t figure out!” Alice sounded exasperated. “I thought it was going to be easy, but it isn’t. Imagine four houses placed on a map and each connected to all the others with a straight road. Now, I was wondering whether the length of every road could be a whole number. That bit is easy! So then I thought about whether the length of every road could be a different whole number. That’s when I got stuck!” Alice slumped in her chair, just to illustrate her defeat.
“Your problem does, indeed, have solutions.” Soothed Professor Pailyn, “But the mathematics needed to find them may take a while to go through. It just means learning some new topics that you probably haven’t yet done in school. We can do it, but your problem has made me think of a similar situation.” The Professor took some paper and sat down next to Alice.
“Your problem does, indeed, have solutions.” Soothed Professor Pailyn, “But the mathematics needed to find them may take a while to go through. It just means learning some new topics that you probably haven’t yet done in school. We can do it, but your problem has made me think of a similar situation.” The Professor took some paper and sat down next to Alice.
OEMO 2001 Advanced Q1: Upper Secondary Mathematics Competition Question
8 Nov 2013
OEMO 2001 Advanced Q4: Upper Secondary Mathematics Competition Question
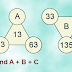
Let A0 = {1, 2} and for n > 0 let An be the set of all numbers that are either elements of An-1 or can be represented as the sum of two distinct elements of An-1.
Further let an = |An| be the number of elements of An.
Determine an as a function of n.
[OEMO 2001 Advanced Q4]
Further let an = |An| be the number of elements of An.
Determine an as a function of n.
[OEMO 2001 Advanced Q4]
7 Nov 2013
Peculiar Pentagon: Upper Secondary Mathematics Competition Question
In a convex pentagon ABCDE the areas of the triangles ABC, ABD, ACD and ADE are all equal to the same value F.
What is the area of the triangle BCE?
[OEMO 2001 Advanced Q3]
What is the area of the triangle BCE?
[OEMO 2001 Advanced Q3]
Between Circles: Middle Secondary Mathematics Competition Question
Three circles of radius 6 cm are arranged as shown in the diagram. A band is placed tightly around the circles. This creates four regions that are bounded by the band but that are external to the circles - these are shown in dark blue.
Find the area highlighted in dark blue.
You may leave your answer as an expression in π.
Find the area highlighted in dark blue.
You may leave your answer as an expression in π.
Ratio of Squares: Lower Secondary Mathematics Competition Question
A large square has a diagonal drawn across it, thereby creating two isosceles triangles. Within each triangle is drawn a smaller square as shown in the diagram.
What is the ratio of the areas of square A to square B?
6 Nov 2013
1 Nov 2013
A Necklace Puzzle: Professor Pailyn's PMQ43
Alice’s mother had bought her a set of beads with which to make some necklaces. Alice had originally frowned upon this as an attempt to give her something girlie-ish. However, she did enjoy making patterns so started playing with the beads. But on this particular day, Alice was getting bored with her pattern-making skills.
"I need to find a really clever pattern; something to impress Zeta. I know just the person to ask."
-=*=-
“OK, let’s start with a simple example. Pick just two colours...”
“Pink and... orange!” Alice interjected.
“Isn’t that a touch... garish?” enquired the Professor.
“It’s not garish... it’s colourful!” beamed Alice. It was, indeed, going to be hideous but it was for her cousin.
“Alright, then pick a maximum length for the beads – let’s pick 3 to make the numbers small.”
“Three! That’s not a necklace, that’s an earring!” Alice was having fun mocking the good Professor. He knew this and happily played along.
“Wait a minute, my impatient child! Now, we’re going to make a necklace where all possible 3-bead permutations exist. How many beads do you think you’ll need?” It was the Professor’s turn to smile with his ‘show-me-how-clever-you-are’ question.
"I need to find a really clever pattern; something to impress Zeta. I know just the person to ask."
-=*=-
“OK, let’s start with a simple example. Pick just two colours...”
“Pink and... orange!” Alice interjected.
“Isn’t that a touch... garish?” enquired the Professor.
“It’s not garish... it’s colourful!” beamed Alice. It was, indeed, going to be hideous but it was for her cousin.
“Alright, then pick a maximum length for the beads – let’s pick 3 to make the numbers small.”
“Three! That’s not a necklace, that’s an earring!” Alice was having fun mocking the good Professor. He knew this and happily played along.
“Wait a minute, my impatient child! Now, we’re going to make a necklace where all possible 3-bead permutations exist. How many beads do you think you’ll need?” It was the Professor’s turn to smile with his ‘show-me-how-clever-you-are’ question.
Subscribe to:
Posts (Atom)